Numerische Simulation von Explosionen und Wirkungen auf die Struktur
Grundsätzlich ist ein Nachweis der Standsicherheit oder Festigkeit einer Struktur experimentell oder rechnerisch möglich. Im experimentellen Fall gibt es ein direktes Ergebnis – bestanden oder nicht bestanden. Der Nachteil dieser Vorgehensweise liegt klar auf der Hand. Ein Apparat oder Teilstruktur muss erst gebaut werden, um diesen dann wieder zu zerstören – wirtschaftlich und zeitlich enorm aufwändig, insbesondere wenn der Test bei Nichtbestehen mehrfach durchgeführt werden muss.
Beim rechnerischen Vorgehen unter Einsatz einer FE-Analyse kann alles virtuell umgesetzt werden. Selbst wenn die Struktur den Belastungen nicht standhält, können Optimierungen zielgenau virtuell durchgeführt werden. Sogar Möglichkeiten der Materialeinsparung lassen sich erörtern und umsetzen.
Bedenken gibt es oftmals bei der Genauigkeit des Berechnungsergebnisses, diese sollen im besten Fall den Versuch sicher ersetzen können. Die Abbildung der Struktur als FE-Modell ist immer mit Modellannahmen verbunden. Insofern gibt es inhärente Unterschiede zwischen Realität und FE-Modell und damit auch bei den Berechnungsergebnissen. Um die FE-Analyse auch bei diesen sicherheitsrelevanten Strukturen einzusetzen, sind jahrelange Erfahrungen der Berechnungsingenieur*innen notwendig. Unterstützung wird den Berechnungsingenieur*innen durch Normen und Richtlinien gegeben.
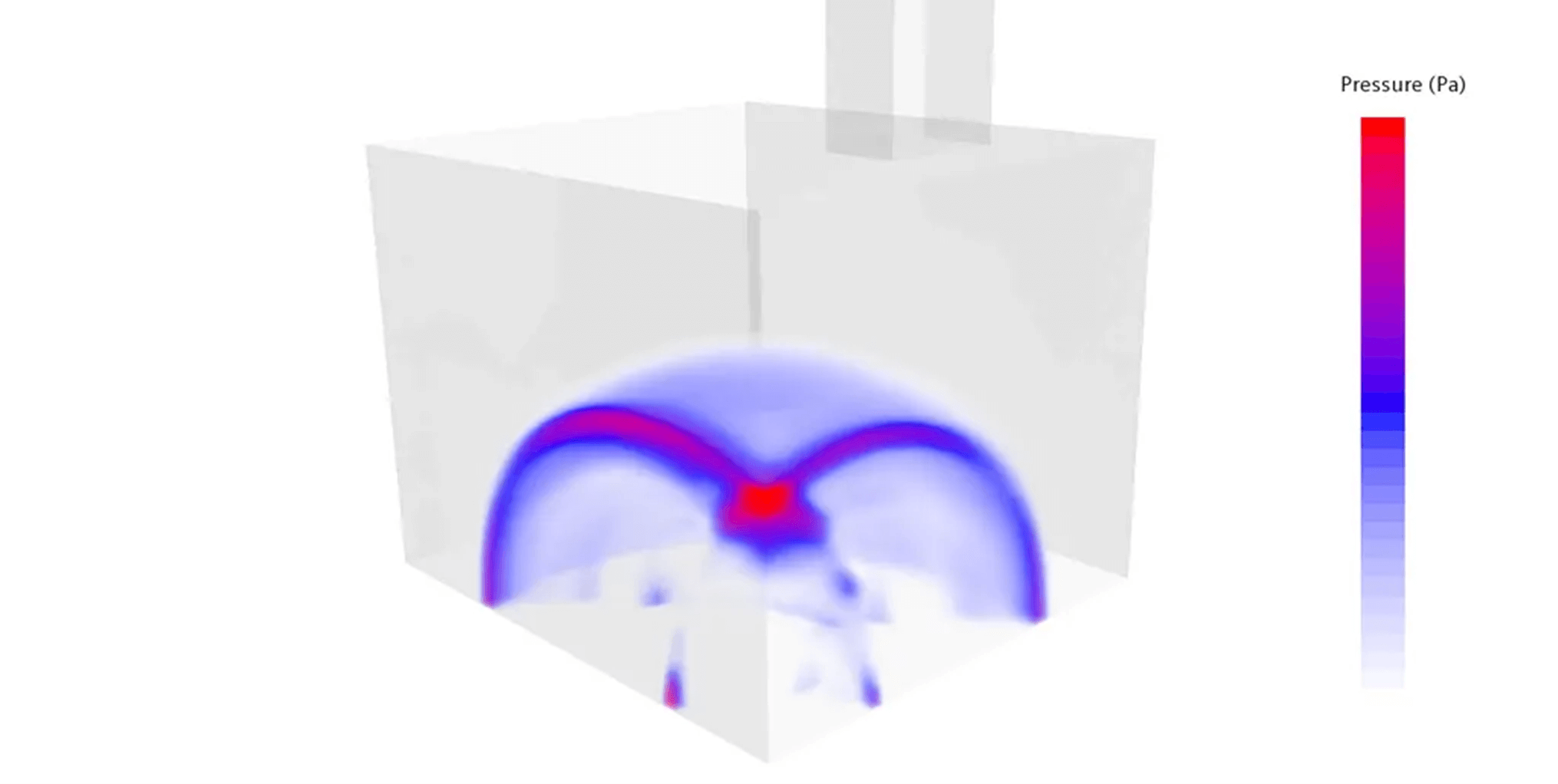
Eine Explosion kann in der Simulation auf unterschiedliche Art und Weise abgebildet werden, über eine transiente hochdynamische Simulation oder über eine quasistatisch vereinfachte Simulation. Beides hat Vor- und Nachteile.
Quasistatische Simulation von Explosionen
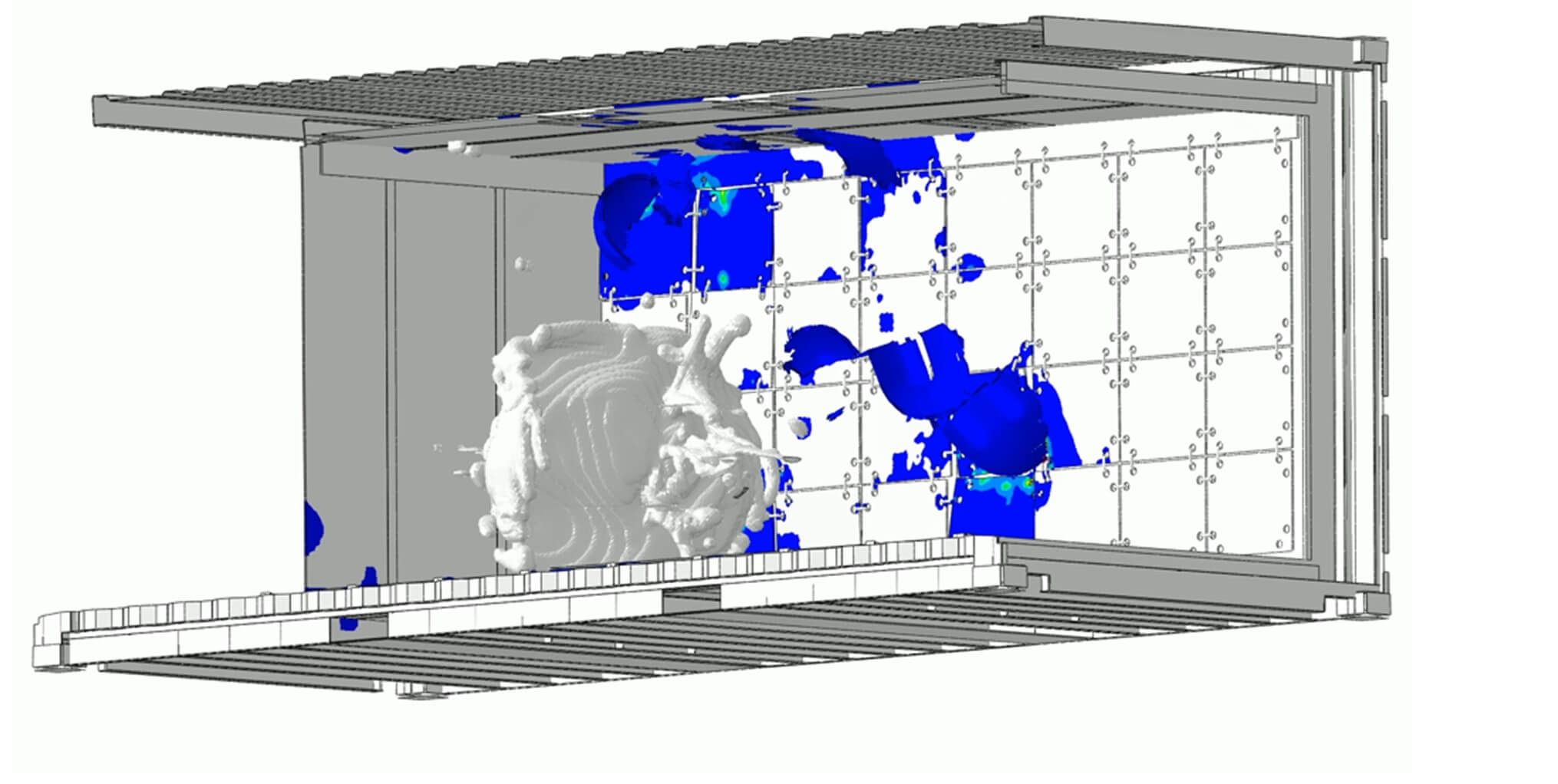
Diese Form der Simulation ist sehr einfach mit einem FE-Modell umzusetzen und wird überwiegend bei Explosionen von Luft/Staub-Gemischen oder Gasgemischen in Filteranlagen, Sichtern, Kanälen oder auch Elektrolyseuren angewendet. Diese reaktionsfähigen Gemische befinden sich innerhalb des Apparates oder der Struktur. Es wird ein Explosionsdruck bzw. im Fall von Druckentlastungen ein reduzierter Explosionsdruck bestimmt. Dieser wird als statischer Druck auf die Druckhülle aufgegeben. Der Explosionsdruck kann mithilfe von Normen, z.B. [DIN EN 14034], [DIN EN 15967], bestimmt werden. Auch bieten die Lieferanten von Druckentlastungsystemen Unterstützung an. Zu beachten sind zusätzlich die Effekte aus Rückstoßkräften und Druckausgleichskräften an Öffnungen des FE-Modells. Auch hierfür gibt es Modellannahmen, z.B. [Steen2000].
Für die Bewertung der FE-Analyse bietet sich die Vorgehensweise der [DIN EN 14460] an. Hier sind auch Angaben zur FE-Modellierung enthalten. Um wirklich die Grenzen der Konstruktion auszunutzen, können die plastischen Tragreserven nach dem Vorgehen der [DIN EN 13445] Teil 3 Anhang B genauer erfasst werden.
Die Vorgehensweise der quasistatischen Berechnung ist sehr einfach umzusetzen und ist in der Regel konservativ. Der Nachteil besteht darin, dass der Ausgangspunkt der Explosion nicht definiert werden kann. Somit sind lokale Explosionen wie z.B. das Bersten von Druckbehältern oder die Explosion einer Batterie nicht abbildbar. Auch kann die Propagation einer Explosionswelle von einer Kammer in die anschließenden Kanäle nicht abgebildet werden.